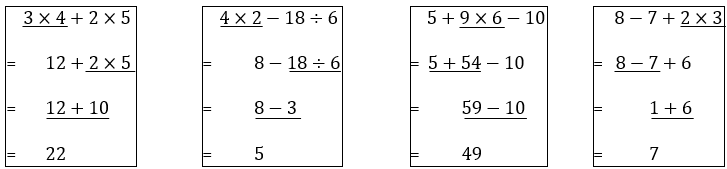Order of Operations (part two)
Hi folks!
Last week, I started breaking down the language of Order of Operations. If you’ve not seen it, please check that out here.
Today, I want to delve into how I get my pupils to lay out their work (at least initially).
1. The highlight of the evening!
There are many ways, when armed with the explanations from last week, that you could ask students to lay out their workings. However, as we have already delved into atomising an expression to find its highest priority, I then like to actually mark this on my paper. (As always, for a captioned version of the image demonstrating this, please send me a reply or comment and I will happily do so)
This is a snippet of I Do examples from my Order of Ops booklet. My description of the first one (using last week’s explanations) would be as follows:
I look for the highest priority operation. I know that I have multiplication and addition. Multiplication has higher priority than addition. However, there are two multiplications. When there are operations of equal priority, I go from left to right. Therefore, I will do 3 times 4 first. On a new line, my 3 x 4 is replaced by 12, and the rest of the calculation remains the same.
From there, I would be explaining the next lines, obviously asking for leaner participation wherever possible. Again, I want to stress that this topic is a primer! Your higher set students will break away from this when they’re ready, including completing multiple calculations at once. This is exactly what we want from them! But, this disciplined, consistent structure means that you can homogenise understanding, and explicitly correct mistakes by using a clear, verbal algorithm. It also will hopefully make them think twice when solving algebraically, which is where this will be heading.
If you’re so inclined, have a go at scripting a full explanation for one of the examples, or challenge your department to do the same and see which ideas sprout from it!
Next week, we will delve into the murky nature of groups, which will hopefully help to banish the nightmare that is substitution and solving the likes of 5x^2!
In the meantime, please comment, share around and let me know any discussions or resources you have found or made regarding any of this!
See you next Monday!