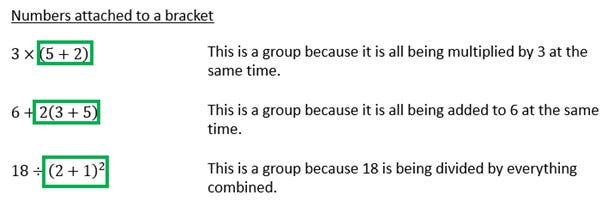Order of Operations (part three)
Hi folks!
Today sees my final post (for now at least) on Order of Operations. Previous entries can be found here and here.
This week, we have a look at operation groups! No, it’s not just brackets, and no, we’re not going to talk about ‘invisible’ brackets either.
1. Supergroups!
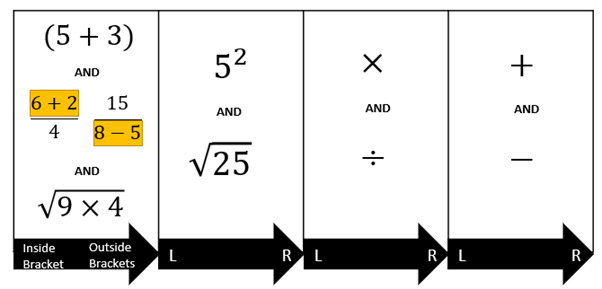
As a reminder, here is my table of operations:
The first column, with the highest priorities, contains my groups. Not only does it contain the much-lauded brackets, but also numerators, denominators, and anything inside a radical. The likelihood is, like me, that you were taught that these others had ‘invisible brackets’. However, this is a bit clunky and, to lower set mathematicians, just infuriating. Is there any way to make them visible? And if not, how on earth do I find the darn things?!
I would love to hear some definitions, but my personal choice is this:
In order of operations, a ‘group’ is a set of numbers (no matter what the symbols) which are all affected by a single operation.
An additional question I pose to encourage thinking about it: can anything outside the group be done before you know the value of the group?
An example explanation is below. As before, if you want a fully captioned version, or indeed the booklet which this came from, please reach out!
This whole thing is, of course, a precursor to difficult substitutions and equations such as 5x^2. So if you can find something that works for your pupils, you can see how valuable getting this right can be!
To really hammer the point home, my first activity isn’t even to solve these groups, it’s to find them, as seen below.
When going through the answers, don’t just ask what they found, ask them to explain their rationale, using that language to justify what they are doing, and to demystify all that rich vocabulary so that everyone can access it.
As always, I would love to hear about any encounters you have with this, either with your students or with your departments. Share your ideas around, and talk about how you can supercharge your explanations to get this through to any learner!
This will be the final post of this term, but I will be back in November, where I will be tackling, among other things, directed/negative number!
Until then, have a restful half term, wherever it may fall, and I look forward to seeing you again!