Order of Operations (part 1)

Hi folks!

This week’s topic is one which is hotly debated at the moment. Order of operations has been scrutinised greatly since I got into teaching, and many people, including Peter Mattock and Kris Boulton, have written extensively about the extent to which order of operations is even necessary in particular situations, depending on mathematical fluency. I want to stress, I am NOT throwing my hat into the ring on that one; I am nowhere near eloquent enough!

However, it is still a topic which we want to get right, and where language can be so ambiguous and contrived. So, how can we make this easier whilst still being memorable?

1. Ditch the acronyms!
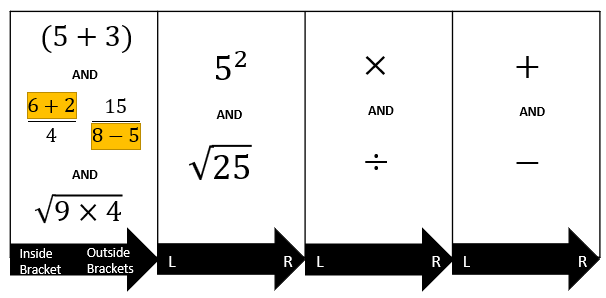
Some cling to them desperately, but honestly there are so many misconceptions in acronyms that anyone who says ‘Well so long as they get it right’ has clearly never tried more than a handful of questions with their students! BIDMAS and its kin have led to so many false assumptions over the years, than entire algorithm of Facebook puzzles was born! Personally, I use a table. It technically most resembles GEMS, but without resorting to American terminology, nor neglecting some operations in their naming. (For those who would like a captioned version, please reply to this email and I will happily provide a written explanation of the image)

The use of the arrows is also to remind students of how to deal with equal priority in the same calculation, going from left to right before treating lesser operations. The use of AND is carefully calculated too, making sure each section is of equal importance, rather than a letter sequence often being misconstrued as a fixed order.

2. Sort out your priorities!
When teaching this topic, I am very careful in the structure of my sentences, and I am highly repetitive both in my own language, and asking students to do the same in their explanations back to me. Rather than describing order of operations, I talk about priority. I find it helps them to zone in on individual pieces of the puzzle, and to think critically when they realise that priority is ambiguous.
For example the first sequence will be focusing on just additions and subtractions in the same calculation, and my written instructions are as follows:

· Addition and subtraction have identical levels of priority.

· When you have a string of additions and subtractions, start from the left and complete one calculation at a time.

· When subtracting, you only subtract the number closest to the symbol.

· If the sequence starts with a positive number, it will have an addition symbol if put anywhere else.

When multiplication and division arrive, notice the similarities and differences:

· Multiplication and division have identical levels of priority.

· When you have a string of multiplications and divisions, start from the left and complete one calculation at a time.

· When dividing, you only divide the number closest to the symbol.

· The number that begins the sequence will have a multiplication symbol if put anywhere else.

Then, we can compare the two:

· Multiplication and division have a higher priority than addition and subtraction.

· When you have a string of calculations with different priorities, calculate the highest priority first from left to right.

· Move on through each level of priority from left to right.

Next week, we will look at some examples and how I set learners’ workings out, before finally tackling the tricky nature of groups! (Spoilers, it’s not just brackets)

In the meantime, please share this with colleagues, and have discussions with your department. Let me know what you come up with!

I will be sharing more snippets from my resources on this, but also please reach out if you would like to see my whole booklet on the topic, or indeed if you would like to compare with resources of your own!

Until then, see you next Monday!