Hi there!
Firstly, this post is the second in my series based on my workshop at Mathsconf34. To read part 1, click here.
In Part 1 I talked about some of the language I use when introducing averages and spread, and the discussion that it sparked in the session. This time, I want to talk about the thoughts I delivered on the sequencing of the topic.
Averages as a topic often seems like something which is often not thought about in granular detail, particularly with regard to the order and manner in which it is taught. With the vast array of complex topics, which algebra and ratio often at the forefront of pedagogical thinking, it is not perhaps surprising that statistics usually takes a back seat. In fact, it has often seemed in my experience that maths departments are brimming with lovers of pure maths and mechanics, but very rarely those of stats.
I hope, at the very least, that these thoughts give you a reason to at least consider how this unit is taught, and perhaps to dedicate some time to the sequencing of more neglected subjects.
In fact, before reading any further, I would like you to ponder this. How do you sequence averages? Is there a particular order for which average is taught first? Is it based on intuition, or on how you were taught at school? Was it the order in which we often list them: mean, median, mode and range? Subsequently, how much of this topic should be taught early on? Do you Year 8s look solely at averages from a list? Are you of the opinion that they already know these from primary, and so go straight to tables (More on that later, it may surprise you!)? Consider writing your thoughts down, on paper or in your Notes app, and come back to them later to drill into them.
So, my opinions - for whatever they are worth.
Firstly, the order in which you introduce the actual averages themselves. As I alluded to in Part 1, there are many linguistic connections between the averages. Combine this with the relative ease and potential for experimentation and scaffolding, I strongly believe that you should consider addressing mode first.
They will be referring to frequency so often, particularly once they get to tables. This immediately introduces the idea of frequency not giving the solution, but showing the location of the true answer. This is true of your three averages, with only range being the exception due to its being a spread and not an average.
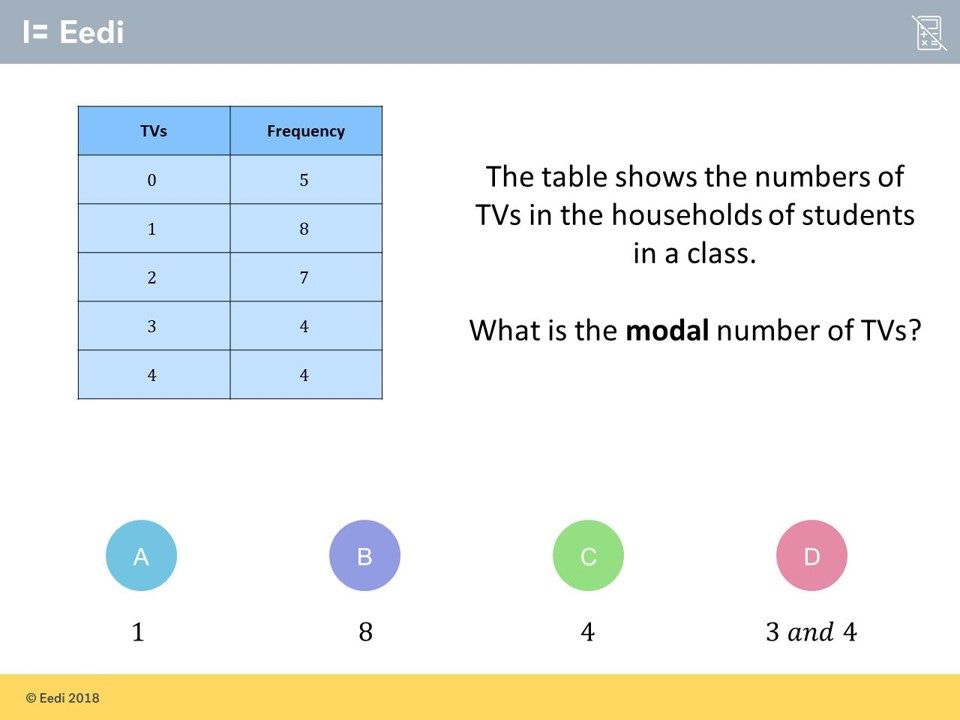
Mode is also fantastic at developing true awareness through examples and non-examples. I love to use tasks asking not only if the mode is correctly identified, but then what are the most common misconceptions for that example. You can build entire banks of questions using the same idea as this Eedi question:
You’ll notice, by the way, that I have gone straight to tables without passing Go on any other averages. This is another idea which I have found useful. Introducing one average in multiple forms not only allows the pupils to become more fluent in finding this average throughout mathematics, but also gives them up to four different opportunities to understand the logic of how lists transfer to tables. Up to 3 chances, then, for retrieval practice just within the week’s sequence, and that many chances for the teacher to pounce on misconceptions and readdress misinterpreted instruction.
So, once I have exhausted mode’s arsenal, I would then move on to mean. This is the average they will likely use more than any other in their mathematical career, and so ensuring it is correct every time is vital. They’ve now seen how an average can be represented in different forms, and are beginning to converse with the proper language to understand why that is the case.
I talked about how there were chances for retrieval. Well, during the You Do (or equivalent) practice session, I would highly recommend making 10-20% of them mode questions. Not just ‘at the end’ or in a cluster together. Keep them on their toes, and apply this throughout the topic. Don’t leave it to the final lesson of the topic to combine these ideas. Examiners certainly won’t!
The final decision in your sequence depends entirely on whether you believe the averages belong together, or whether spread is taught at the same time. Either way, though, median should be the final of your three averages. Simply put, it is the most difficult. Lots of exceptions, very algorithmic thinking, and a demand in fluency with language to really get to grips with how to decipher it all. Build pupils’ confidence first in finding mode or mean under any circumstance, because they will need it to fully grasp median.
Now, in a display of narrative resolution, I will go back to the idea of students already knowing averages from lists from Key Stage 2. I was equally a believer in this, until Jo Morgan shared her deep dive into the KS2 curriculum. If you get a spare 45 minutes (which I will assume you don’t have at the time of reading), then it is essential knowledge for anyone looking at their KS3 sequencing and prior knowledge.
In short, this is the entirety of Statistics at KS2:
Surprising when you see it for the first time, isn’t it? Mean is the only average which should be taught at primary. Therefore, we must assume either that our pupils have no working knowledge of any others, or that if they were, they were introduced by someone as more of a follow-up challenge, or by someone they know who wanted to expand their education. This means that we must tread carefully, and that starting with ‘so, who’s heard of these averages?’ could actually be harmful in stopping the spread of common misconceptions. “Isn’t it the middle one sir?”, “Most common…I think?”, “Oh that’s easy, add them up and divide by how many there are. Oh, this table’s weird!”
So, as a final recap, here was the slide I showed detailing how I like to order the topic:
I hope, even if you disagree with any of these opinions, that it sparks some reflection in your practice, even if it’s not this topic! If you haven’t already, look back at your notes from earlier. Has anything changed? Have your own ideas now been reinforced through thinking about them? I would love to hear any feedback or ideas of your own which have come from this. Please feel free to reply here, or on socials, and spread your thoughts. Equally, if you have any questions, please get in touch! Again you can reply here, @jwrightmaths on Twitter, or jwrightmaths@gmail.com
I may come back to this if there is interest in a Part 3/Epilogue, but I also have several ideas in the pipeline, so you may see a mix of stuff over the coming weeks. Please let me know if there are any things you would like me to cover, especially relating to mathematical language and modelling. But until then, enjoy the rest of your bank holiday and hopefully see you next Monday!




This has been really helpful. I’ve struggled with the teaching of this topic in the past although in my current role there is often little actual teaching and more just unraveling the misconceptions that have developed, often through the language that as been used in the tutees’ classroom. This sequence makes a lot of sense!